近日,信息科学与工程学部物理与光电工程学院周龙文教授及其合作者在驱动系统的拓扑量子临界态研究中取得进展,相关成果发表于Nature出版社旗下刊物《Communications Physics》(1区,TOP期刊)。
拓扑物态是物理学近五十年最受关注的研究领域之一。拓扑物相理论是现代凝聚态物理学的基石,其内涵已超越基于对称性破缺序的Landau-Ginzburg-Wilson范式。对称保护拓扑(SPT)相作为拓扑态的典型代表,通常与体态能隙相关联。传统观点认为当体能隙闭合时,SPT相的拓扑特性将消失。然而近期研究表明,拓扑物理的诸多核心特征(如拓扑边缘模)能与体态临界涨落共存,这一认识催生了对量子临界点处非平庸拓扑特征的定义,即当前学界所称的拓扑非平庸量子临界点或无能隙SPT相。对伴随能隙闭合而存在的拓扑保护边缘态的发现表明,拓扑特征在相变分类以及相边界上的拓扑相变探测中仍起关键作用,这也为量子相变研究开辟了新方向。
非平衡系统(尤其是与量子模拟实验密切相关的体系)能展现诸多静态系统中不存在的新奇拓扑现象。作为非平衡体系的范例,人们已经在周期驱动(Floquet)系统中实现了Floquet拓扑相、Floquet多体局域化及离散时间晶体等多种非平衡物态,大大拓展了量子物理和统计物理的研究前沿。在相关研究中,一个很重要但尚未被系统解决的问题是:拓扑保护的边缘态(其本身可能不存在静态对应物)能否与Floquet准能隙闭合(即Floquet量子临界性)共存?解决这一问题有望为构造和调控量子计算中受拓扑保护的量子比特提供重要的理论支撑。
在该工作中,周龙文教授及其合作者对一大类周期驱动马约拉纳费米子链进行了理论研究,解析求解了其拓扑边缘模存在于拓扑相边界的条件,发现这类体系的拓扑相图具有普适结构。基于此,研究者们成功构建了具有任意多个马约拉纳边缘模的系统——这些边缘模不仅存在于拓扑超导相中,还能持续存在于拓扑相边界上(即与无能隙Floquet体态共存,因而称为临界Majorana边缘模)。此外,研究者们发现在拓扑相边界上不仅存在已知的临界Majorana零模,更具有一种非平衡系统独有的临界Majorana π模。通过引入一组基于柯西辅角定理的广义拓扑绕数,研究者们构建了描述一维Floquet量子临界系统中体-边对应的一般规则,并将研究结果推广至二维非平衡陈绝缘体系统,通过数值计算验证了理论的普适性。
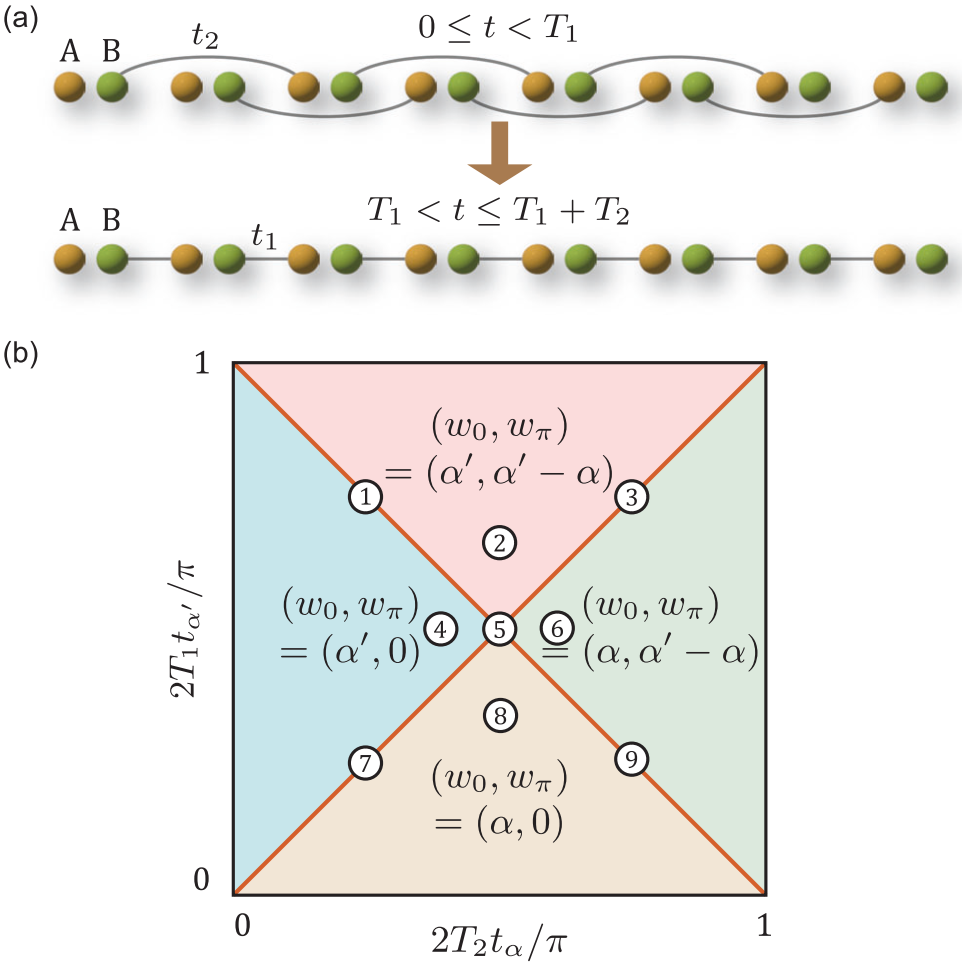
Floquet马约拉纳链的晶格模型(a)与拓扑相图(b)
该论文的第一作者为周龙文教授,第一作者单位为中国海洋大学。论文的合作者和通讯作者为新加坡国立大学龚江滨教授和福州大学余雪佳教授。该研究工作受到国家自然科学基金面上项目等项目资助。
周龙文教授2011-2018年在新加坡国立大学物理系获得博士学位并从事博士后研究,2018年加入中国海洋大学顾永建教授的量子物理研究团队,近年来致力于带领其研究组探索Floquet拓扑态、非厄米物理、动力学量子相变等量子物理和凝聚态物理中的前沿理论课题,在PRL、PRB等期刊发表论文50余篇,谷歌引用2100余次,H因子30,2024年曾入选全球前2%顶尖科学家影响力榜单和中国科学院理论物理研究所青年访问科学家项目。
原文链接:https://www.nature.com/articles/s42005-025-02137-7
通讯员:潘家欣
初审:徐君岭
终审:宋青


