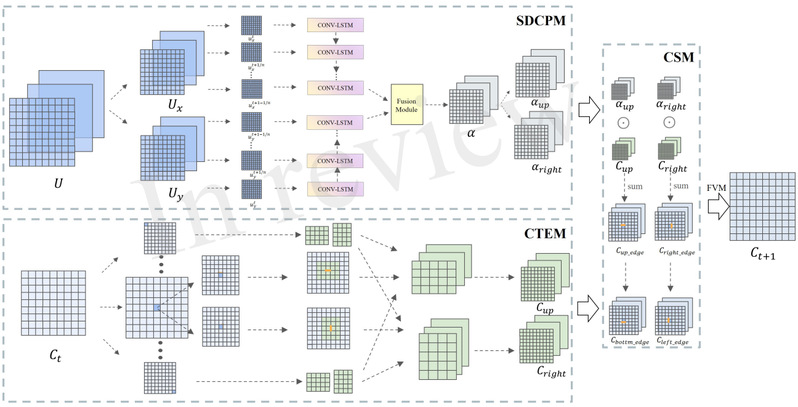
流体的数值模拟是一个巨大的挑战,因为它包含了极其复杂的高雷诺数变化,通常需要非常高分辨率的网格来捕捉其物理过程中非常细微的变化,以实现精确的模拟,这将导致大量的计算。这一问题长期以来一直是深度学习的瓶颈问题,直到深度学习的解决方案提出,在空间离散化过程中使用自适应调整系数的大尺度网格,而不是传统的固定系数的小网格,从而大大降低了计算成本,并保持了精度。这一突破被认为是流体数值模拟的重大改进。然而,以往提出的基于深度学习的方法在预测系数时往往只考虑网格之间的空间相关性,提供的上下文相对有限,不能充分描述时间维度上的模式,这意味着系数的时空相关性不能很好地学习。为了解决这个问题,我们提出了涉及时间序列的空间离散化神经网络(TSI-SD)来同时从空间和时间视图中提取网格相关性。这种新型的深度神经网络是由经典的conv-lstm主干转换而来的,在第一步将时间信息分别沿x轴和y轴添加到二维空间网格中,然后通过融合神经网络将其融合。在此基础上,我们将TSI-SD与有限体积格式相结合,作为二维不稳定流中的被动标量平流求解器。与以往只考虑空间上下文的方法相比,我们的方法可以获得更高的仿真精度,同时也减少了计算量,因为我们发现,在空间离散化过程中,输入特征之一的时间数据加入后,浓度场是冗余的,不应该再采用,这使得参数尺度急剧下降,效率很高。通过与SOTA方法的对比和充分的消融研究,验证了所提方法的准确性和有效性,并讨论了所提方法的优点。